Csound Tutorial 4

Following from yesterday’s tutorial, we can now create a sine oscillator, alter the pitch, and even apply an amplitude envelope on each of the notes. But what would be really kool is if we could actually create a more interesting sonic output than a plain sine tone…

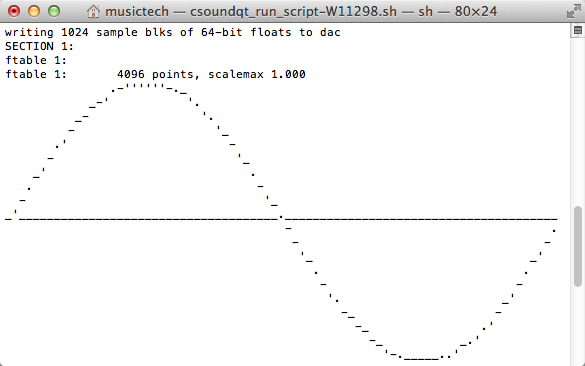
Remember the frequency table f1?

f1 0 4096 10 1

Here f1 is created at time = 0, has a buffer size of 4096, uses GEN10 subroutine, and has the value 1. From the manual, we know GEN10 generates composite waveforms made up of the weighted sums of simple sinusoids. As the waveform only consists of the fundamental (i.e. first partial has value 1), a simple sine tone is generated. This can be verified by pressing ‘run in term’ and seeing the resulting ASCII graphic:

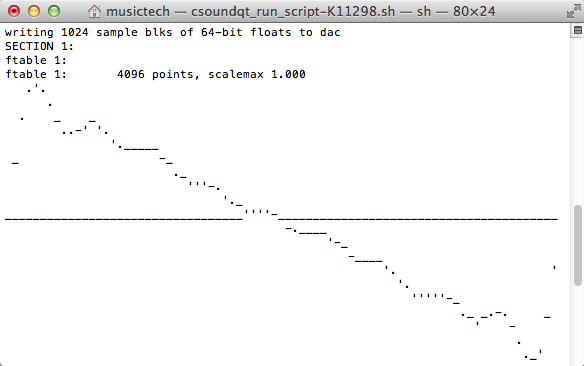
Thus we can create different timbre instruments by experimenting with the amplitude of the harmonics, for instance 

f2 0 4096 10 1 0.5 0.3 0.25 0.2 0.167 0.14 0.125 .111

creates a sawtooth wave

But that’s not all! We aren’t limited to only having one oscillator per instrument, and can in fact combine them to create a new, exotic sound!

<CsoundSynthesizer>

<CsInstruments>
	sr     = 44100					;sample rate
	kr     = 4410					;control signal rate
	ksmps  = 10					;samples per control signal
	nchnls = 1					;number of output channels

		instr 1
	k1	linen	ampdb(p4), 0.005, p3, 0.005	;amplitude envelope with 5ms fade-in and fade-out time
	a1	oscil 	k1, p5, 1			;uses function table 1
	a2	oscil 	k1, p5, 2 			;uses function table 2
		out 	0.6*a1 + 0.4*a2			;summed output
		endin

</CsInstruments>

<CsScore>

	;fn 	time 	size 	gen 	parameters
	f1 	0 	4096 	10 	1 						; Sine
	f2 	0 	4096 	10 	1 0.5 0.3 0.25 0.2 0.167 0.14 0.125 .111 	; Sawtooth
	f3 	0 	4096 	10 	1 0   0.3 0    0.2 0     0.14 0     .111 	; Square
	f4 	0 	4096	10 	1 1   1   1    0.7 0.5   0.3  0.1 		; Pulse

	;ins	strt	dur(p3)	amp(p4)	freq(p5)
	i1   	0	1		90 		440
	i1   	1	1		75		528.64
	i1   	2	1		.		594.39
	i1   	3	1		60		660
	i1   	4 	1		75		792.86
</CsScore>

</CsoundSynthesizer>

Here we create two audio variables a1 and a2 which are both subjected to an amplitude envelope (to avoid popping) and reference function tables #1 and #2 respectively. These audio values are then weighted 60-40 and summed together to generate the final audio output.

Also, as amplitude values of 100000, 3162 etc. are quite abstract, we can use the function ampdb to translate a decibel (dB) value into the amplitude equivalent. Finally, the special character ’.’ can be used to signify that the parameter in the current column is the same as the row above, thus the amplitude of the note with frequency 594.39 Hz is 75dB.

In this fourth tutorial, we have injected some timbre variation into our previous static sine wave. Next week we will consider how to go beyond the static Csound score.